Calculators » Band Pass Filter Calculator | Electronics Design

Band Pass Filter Calculator | Electronics Design

band pass filter calculator filter design bandpass filter formula electronic filter design

This Band Pass Filter Calculator helps you design band pass filters by calculating key parameters such as center frequency (Fc), bandwidth (BW), and quality factor (Q) based on your input component values. Whether you’re working on analog circuits or RF applications, this tool simplifies the design process.

A series RLC circuit can function as a band pass filter by taking the output voltage across the resistor. This configuration allows frequencies near the circuit’s resonant frequency to pass through while attenuating frequencies above and below that range

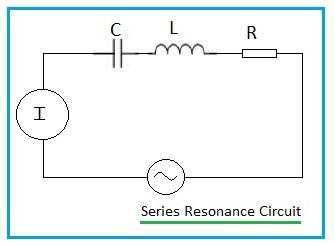
Series Resonance Circuit

Band Pass Filter Calculator

Inputs

Outputs

EXAMPLE:

  • INPUTS:

    • Resistor (R) : 100 Ohms
    • Inductor (L) : 100 mH
    • Capacitor (C) : 1 uF

  • OUTPUT:

    • Fc (Center Frequency) : 0.50 KHz
    • BW (Bandwidth) : 0.16 KHz
    • Q (Quality Factor) : 3.16

Band Pass Filter Formula

Band Pass Filter Formula

Where,

  • Fc = Center Frequency (Hz)
  • BW = Bandwidth (Hz)
  • Q = Quality Factor
  • R = Resistance (Ohms)
  • L = Inductance (Henrys)
  • C = Capacitance (Farads)
  • π = Pi (approximately 3.14159)

Applications of Band Pass Filters

Series RLC band pass filters (BPFs) are widely used in various applications due to their frequency selective properties.

  1. Radio and TV tuning circuits: Used to select a specific narrow frequency band from ambient radio waves.
  2. Wireless Communication: In transmitter and receiver circuits to pass only required signals and reduce interference.
  3. Signal Processing: In medical instruments (like EEGs) and other systems to isolate specific frequencies of interest.

Summary

The Band Pass Filter Calculator is an essential tool for engineers and hobbyists looking to design effective band pass filters. By inputting component values, users can quickly obtain critical parameters such as center frequency, bandwidth, and quality factor, facilitating efficient and accurate filter design for various applications.

References

  • “Electronic Filter Design Handbook” by Arthur B. Williams and Fred J. Taylor
  • Alexander, C. K., & Sadiku, M. N. (2012). Fundamentals of Electric Circuits. McGraw-Hill Education.