Snell's Law Calculator | Refraction Angle Tool

This tool calculates the refraction angle of light as it passes from one medium to another using Snell’s Law.

Snell’s Law relates the angles of incidence and refraction when light passes through different media, based on their refractive indices. It is expressed mathematically as:

$n_1 \sin(\theta_1) = n_2 \sin(\theta_2)$

It is widely used in optics to predict how light will bend when transitioning between materials with different refractive properties, such as air to water or glass to air.

Refraction Angle Calculation

EXAMPLE:

Light travels from water (n1 = 1.33) into air (n2 = 1.00) at an incident angle of 30 degrees. Calculate the refraction angle.

• INPUTS:

  • Refractive index of medium 1 (n1) = 1.33
  • Refractive index of medium 2 (n2) = 1.00
  • Incident angle (θ1) = 30 degrees

• OUTPUT:

  • Refraction angle (θ2) ≈ 41.68 degrees

Snell’s Law Formula for Refraction Angle

The following equation or formula is used to calculate the refraction angle using Snell’s Law:

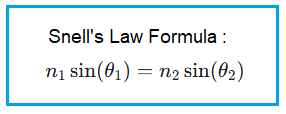
Where:

• n1 = Refractive index of medium 1
• n2 = Refractive index of medium 2
• θ1 = Incident angle (angle of incidence)
• θ2 = Refraction angle (angle of refraction)
• sin = Sine function

Applications with benefits

1. Design of Optical Lenses

• Application: Snell’s Law is used to design lenses in cameras, microscopes, telescopes, and projectors by predicting how light rays bend inside glass or plastic.
• Benefits: Produces sharp and clear images, Allows correction of vision defects

2. Vision Correction (Eyeglasses & Contact Lenses)

• Application: Lens shapes are calculated using Snell’s Law to ensure light focuses correctly on the retina.
• Benefits: Improves eyesight for millions of people, Reduces eye strain and headaches, Provides customized vision correction

3. Fiber Optic Communication

• Application: Snell’s Law explains total internal reflection, which allows light signals to travel long distances through optical fibers.
• Benefits: High speed internet and data transmission, Minimal signal loss, Supports modern communication systems

4. Medical Imaging and Instruments

• Application: Endoscopes and optical diagnostic tools rely on controlled refraction of light for internal imaging.
• Benefits: Enables non-invasive diagnosis, Improves accuracy of medical procedures, Enhances patient safety

5. Underwater Viewing and Navigation

• Application: Snell’s Law explains why objects underwater appear closer or distorted when viewed from air.
• Benefits: Helps divers and submarine operators judge distance correctly, Improves underwater photography, Enhances safety in marine navigation

6. Prism and Spectrometer Design

• Application: Prisms use refraction to separate light into different wavelengths using Snell’s Law.
• Benefits: Helps analyze chemical compositions, Used in laboratories and research, Aids in astronomical observations

7. Laser Technology

• Application: Snell’s Law guides how lasers are directed through lenses and optical components.
• Benefits: Precise targeting in surgery and industry, Efficient energy control, High accuracy in cutting and measurement

8. Atmospheric Science (Mirages & Refraction)

• Application: Snell’s Law explains bending of light in air layers of different temperatures.
• Benefits: Helps understand mirages and optical illusions, Improves weather observation models, Enhances aviation safety

Summary

By inputting the refractive indices and incident angle into Snell’s Law, you can calculate the refraction angle when light passes between different media. This is essential for understanding light behavior in optics.

References

• Snell’s Law - Wikipedia
• Optics and Refraction - HyperPhysics
• Refractive Index - Encyclopedia Britannica