Kepler’s First, Second & Third Laws: Satellite Applications

Kepler’s First Law

“The orbit of every planet is an ellipse with the Sun at one of the two foci”. The same has been shown in the figure-1.

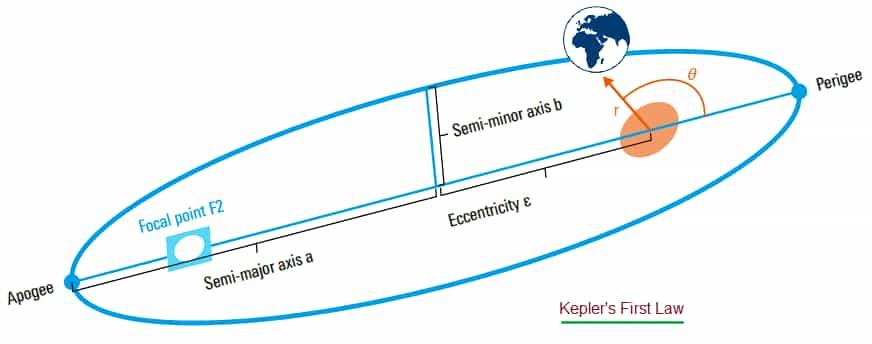Image Courtesy : Rohde & Schwarz

Application : Satellites used in NTN (e.g., LEO, MEO, GEO) follow orbital paths around Earth (or roughly so) and their orbits may be elliptical (or approximately circular, which is a special case of ellipse with low eccentricity).

Kepler’s Second Law

“A line joining a planet and the Sun sweeps out equal areas in equal amounts of time”. The same is shown by figure-2 and can be expressed by the equation mentioned in the figure-2.

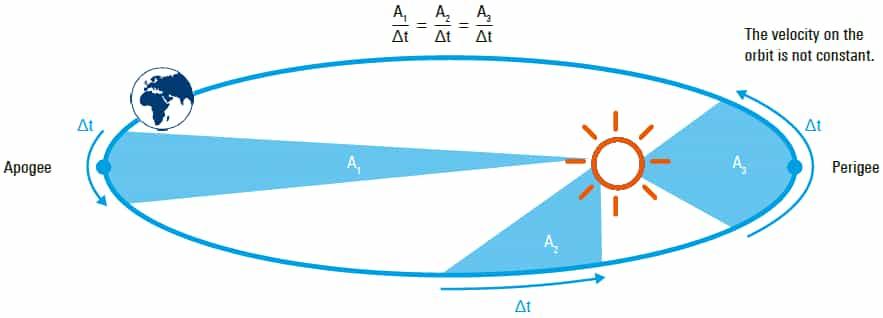Image Courtesy : Rohde & Schwarz

Application : Because the line joining the satellite to the Earth (or ground station or UE) sweeps out equal areas in equal times, the satellite’s speed varies depending on its orbital position (closer vs farther) in an elliptical orbit.

• Second law reminds network designers that speed is not constant and that “cells” served by a moving satellite will change footprint and link characteristics over time - thus requiring dynamic adaptation.

Kepler’s Third Law

“The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit”. Symbolically.

$T^2 ∝ a^3$

Where, ’𝑇’ is the orbital period and ‘a’ is the semi-major axis (average size) of the orbit.

• This law provides a precise mathematical relationship between the size of a satellite’s orbit (its altitude, defined by the semi-major axis) and the time it takes to complete one full orbit (the orbital period).
• Third law supports the system-level design of NTN constellations (how many satellites, orbit altitudes, coverage dwell times, cell hand‐over rates) by linking orbit size to period/dwell time.